7 minutos de lectura
Hallan patrones en composiciones de Bach
El músico alemán Johann Sebastian Bach (1685- 1750) es uno de los compositores más admirados en la historia de la música clásica.
Pero ¿se podrían cuantificar y comprender sus partituras de una manera objetiva?
En estudios recientes se ha empleado la teoría de la información, específicamente la entropía de Shannon, para buscar estructuras y patrones presentes en sus obras que podrían interpretarse y proporcionar información específica.
La música de Bach como conjunto de datos
Bach es reconocido como uno de los mayores compositores de todos los tiempos.
Se lo identifica como uno de los grandes maestros en la creación de piezas de música clerical e instrumental.
Sus más de mil piezas musicales representan lo mejor de la era barroca.
Algunas de las obras más famosas de Bach son El Concierto de Brandenburgo Nº 1, El clave bien temperado y la Misa en si menor.
La sofisticación de la belleza, la amplia diversidad de elementos entrelazados y abstracción de las composiciones de Bach han motivado el estudio de sus obras.
Sus composiciones muchas veces se comparan con fórmulas matemáticas.
Cada partitura representa estructuras musicales complejas y organizadas.
El objetivo del análisis matemático de la obra de Bach es comprender el trasfondo de cada una de estas partituras.
Figura 1
Retrato de Johann Sebastian Bach

Nota. Adaptado por Plaza Cielo Tierra de Retrato de Johann Sebastian Bach {Pintura}, Elias Gottlob Haussmann, 1748, Wikipedia (https://es.m.wikipedia.org/wiki/Archivo:Johann_Sebastian_Bach.jpg ). CC0.
Cuando se escucha música se crean expectativas. Al oír una nota concreta, quienes escuchan anticipan qué notas podrían venir a continuación basándose en transiciones anteriores. Cuanto menos probable es el resultado, más se sorprenden al escucharlo.
Esta sorpresividad puede cuantificarse mediante la teoría de la información, específicamente la Teoría Matemática de la Información propuesta por el estadounidense Claude Shannon (1916-2001) , ya que puede ofrecer una nueva perspectiva analítica para entender qué tipo de información matemática ocultan estas composiciones.
Eso es lo que sostienen los físicos y bioingenieros de las Universidades de Pensilvania y de Princeton, así como especialistas en psicología de la Universidad de Yale y teóricos de las ciencias de la Universidad de Nueva York en el estudio Information content of note transitions in the music of J. S. Bach publicado en Physical Review Research en febrero de 2024.
Asimismo, para construir un marco de partida para estudiar la información transmitida por una pieza musical, aquel equipo de científicos estadounidenses emplearon también ideas de la ciencia de redes y de la física estadística.
La teoría de la información
El término “información” puede asociarse a diferentes significados.
La noción de información que desarrollaron en su teoría matemática de la comunicación el matemático, ingeniero eléctrico y criptógrafo Claude Shannon y el matemático Warren Weaver en la década de 1940, define a la información como un cuantum medible. En relación inversa con la probabilidad de ocurrencia de los caracteres físicos que lo componen.
Por ejemplo: en castellano, la letra «ñ» contiene más información que la letra “a”, y el término “que” contiene menos información que el término “desoxirribonucleico”.
Para la teoría matemática de la información, la preocupación es cómo lograr que un conjunto X de signos llegue con rapidez y con la menor pérdida de un extremo al otro de un canal habitualmente imperfecto, no importa qué se diga en ese mensaje.
La entropía
En términos simples, cuanto más impredecible es un conjunto de datos, mayor es su entropía y más información se tiene.
Por el contrario, cuanto más predecible es un conjunto de datos, menor es su entropía y menor información se puede obtener.
El concepto entropía se aplica en termodinámica, electrónica, mecánica estadística y teoría de la información.
Figura 2
Claude Shannon

Nota. Adaptado de Claude Shannon por Plaza Cielo Tierra {Fotografía] de Jacobs Konrad, Instituto de Investigación Matemática de Oberwolfach (https://opc.mfo.de/detail?photo_id=3807 ). Creative Commons Attribution-Share Alike 2.0 Germany license.
Pero entonces, pensando en las partituras de Bach, que contienen una estructura organizada y con patrones reconocibles, ¿se podría cuantificar la información contenida en sus obras?
La entropía de Shannon y las partituras de Bach
En el estudio antes mencionado, en base a la idea de entropía de Shannon se analizaron las partituras de Bach ya que contienen información cuantificable.
El análisis se realizó a diferentes estilos: preludios, fugas, invenciones, cantatas, suites inglesas, suites francesas, corales, conciertos de Brandenburgo, tocatas y conciertos.
El procedimiento para analizarlas fue el siguiente: a partir de cada partitura se armó una red representada por puntos y líneas, donde los puntos, llamados nodos, son representaciones de las notas y las líneas, llamadas aristas, son las representaciones de cada transición entre dos notas.
Diferentes partituras contienen una cantidad específica de nodos y una cantidad específica de aristas. Por lo tanto, las redes construidas a partir de ellas fueron diferentes de una partitura a otra.
La idea fue analizar estas redes y de ahí cuantificar la información reconociendo patrones y secuencias en ellas.
Figura 3
Ejemplos de redes correspondientes a diferentes composiciones
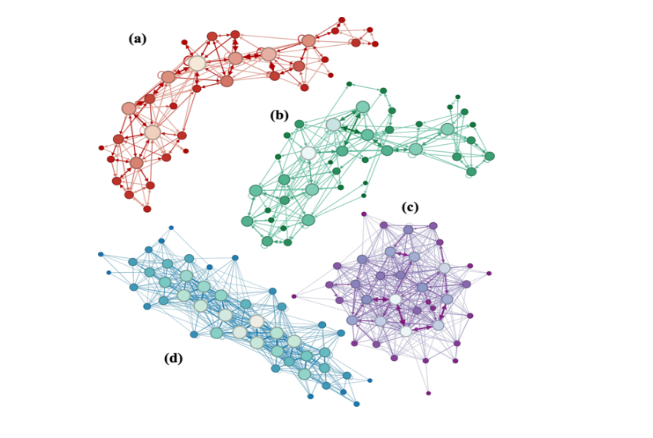
Nota. Adaptado de ”Information content of note transitions in the music of J. S. Bach” por Kulkarni, S., David S. U., Lynn C. y Bassett D., Physical Review Research, 6 (1).
Asimismo, para comprender mejor la cantidad de información se compararon las redes construidas a partir de las partituras con redes aleatorias (o “nulas”) del mismo tamaño.
Lo que se obtuvo de este análisis fue, en primer lugar, que la información de las redes musicales tienen una entropía mayor que las redes aleatorias.
Por lo tanto, más información.
Pero por otro lado, se observó que los diferentes tipos de composiciones se pueden agrupar según su cantidad de información y estructura de red.
Por ejemplo, los corales que son piezas más breves y sencillas mostraron menor entropía que el resto de las composiciones analizadas.
En contraparte, las tocatas, que son piezas más complejas y abarcan un mayor rango melódico, mostraron una entropía mucho mayor.
Conclusiones
Si bien los estudios realizados hasta ahora no son suficientes para dar una conclusión definitiva, este método permitió mostrar un nuevo trasfondo de las partituras de Bach, dando lugar al aspecto informacional que existe dentro de ellas.
La entropía de Shannon sería una herramienta que podría sumarse al estudio musical para dar una nueva perspectiva que complemente con su entendimiento y análisis.
Referencias bibliográficas
-
Suman Kulkarni, S., David, S. U., Lynn, C. y Bassett D. S. (2023). Information content of note transitions in the music of J. S. Bach. Physical Review Research. Volumen (6). https://doi.org/10.1103/PhysRevResearch.6.013136
-
Febres, G. y Jaffe, K. Music viewed by its entropy content: A novel window for comparative analysis. Plos One. 12 (10). https://doi.org/10.1371/journal.pone.0185757
-
Lombardi, O. Información de Shannon: Bases teóricas, articulaciones conceptuales e interpretaciones. Ápeiron Estudios de Filosofía. Volumen 12.
https://orcid.org/0000-0003-2204-7902
-
Erill Soto, B. (2024). El secreto matemático de las partituras de Bach. National Geographic. https://historia.nationalgeographic.com.es/a/mensajes-escondidos-partituras-bach-segun-metodos-cientificos_20895